|
ola aqui les traigo esto
Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.
Una expresión algebraica es una combinación de letras y números ligadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación.
Las expresiones algebraicas nos permiten, por ejemplo, hallar áreas y volúmenes.
Longitud de la circunferencia: L = 2 r, donde r es el radio de la circunferencia. r, donde r es el radio de la circunferencia.
Área del cuadrado: S = l2, donde l es el lado del cuadrado.
Volumen del cubo: V = a3, donde a es la arista del cubo.
Expresiones algebraicas comunes
El doble o duplo de un número: 2x
El triple de un número: 3x
El cuádruplo de un número: 4x
La mitad de un número: x/2.
Un tercio de un número: x/3.
Un cuarto de un número: x/4.
Un número es proporcional a 2, 3, 4, ...: 2x, 3x, 4x,..
Un número al cuadrado: x2
Un número al cubo: x3
Dos números consecutivos: x y x + 1.
Dos números consecutivos pares: 2x y 2x + 2.
Dos números consecutivos impares: 2x + 1 y 2x + 3.
Descomponer 24 en dos partes: x y 24 − x.
La suma de dos números es 24: x y 24 − x.
La diferencia de dos números es 24: x y 24 + x.
El producto de dos números es 24: x y 24/x.
El cociente de dos números es 24; x y 24 · x.
Valor numérico de una expresión algebraica
El valor númerico de una expresión algebraica, para un determinado valor, es el número que se obtiene al sustituir en ésta por valor numérico dado y realizar las operaciones indicadas.
L(r) = 2 r r
r = 5 cm. L (5)= 2 ·  · 5 = 10 · 5 = 10 cm cm
S(l) = l2
l = 5 cm A(5) = 52 = 25 cm2
V(a) = a3
a = 5 cm V(5) = 53 = 125 cm3
Tipos de expresiones algebraicas
Monomio
Un monomio es una expresión algebraica formada por un solo término.
Binomio
Un binomio es una expresión algebraica formada por dos términos.
Trinomio
Un trinomio es una expresión algebraica formada por tres términos.
Polinomio
Un polinomio es una expresión algebraica formada por más de un término.
Expresiones Algebraicas. Polinomios
| |

 |
 |
 |
 Qué es una expresión algebraica Qué es una expresión algebraica |
|
Los padres de Iván le han encargado que vaya al mercado a comprar 4 kg de naranjas y 5 kg de manzanas. Pero no saben lo que cuesta cada tipo de fruta.
Si llamamos x al precio del kilo de naranjas, e y al precio del kilo de manzanas, podemos decir que:
COSTE TOTAL = 4 · x + 5 · y
La expresión 4 · x + 5 · y es una expresión algebraica.
|
 |
 |
 |
 Una expresión algebraica es una combinación de números y letras unidos por los signos de las operaciones aritméticas. Una expresión algebraica es una combinación de números y letras unidos por los signos de las operaciones aritméticas.
Ejemplos de expresiones algebraicas son: 3x2 + 7y, 5c2y, x − 3y, ...
|
|
|
|
Una vez en el mercado, Iván se encuentra con dos fruterías.
En cada una le ofrecen precios distintos, así que Iván está intentando hacer cuentas.
¿En cuál de estas dos fruterías le saldrá más barata la compra |
 |
Vamos a intentar ayudar a Iván haciendo cuentas también nosotros:
FRUTAS GÓMEZ
Naranjas 1,40 €/kg - Manzanas 1,90 €/kg |
FRUTERÍA OTERO
Naranjas 1,50 €/kg - Manzanas 1,80 €/kg |
x = 1,4 y = 1,9
Sustituyendo estos valores en la expresión algebraica inicial, obtenemos:
4x + 5y = 4 · 1,4 + 5 · 1,9 = 15, 1 |
x = 1,5 y = 1,8
Sustituyendo estos valores en la expresión algebraica inicial, obtenemos:
4x + 5y = 4 · 1,5 + 5 · 1,8 = 15 |
Por tanto, Iván gastaría 15,10 € en "Frutas Gómez". 15,10 es el valor numérico de 4x + 5y para x = 1,4; y = 1,9.
Igualmente, gastaría 15 € en "Frutería Otero". Por tanto, 15 es el valor numérico de 4x + 5y para x = 1,5; y = 1,8.
 |
 |
 El valor numérico de una expresión algebraica es el valor que se obtiene al sustituir las letras por números determinados y efectuar las operaciones que indique la expresión. El valor numérico de una expresión algebraica es el valor que se obtiene al sustituir las letras por números determinados y efectuar las operaciones que indique la expresión. |
|
| |

¿Recuerdas la propiedad del producto de potencias de la misma base?
|
|
 El producto de monomios es otro monomio que tiene: El producto de monomios es otro monomio que tiene:
- Como coeficiente, el producto de los coeficientes.
- Como parte literal, las letras de los monomios multiplicados, con un exponente igual a la suma de los exponentes de los factores.
Lenguaje algebraico a lenguaje verbal
Enuncia verbalmente las siguientes expresiones algebraicas:1. x 2 : "La diferencia entre un número y 2"2. 2x3. x + 34. 2x + 55. 2x³6. x 3y7. x²8. 5x9. x + y10. 2x 3y²11. (2x)²12. (4x)³13. (x 1)²14. (x + y)³
EXPRESIONES ALGEBRAICAS
1. Determina el coeficiente numérico y el parte literal de los siguientes términosalgebraicos:Término algebraico Coeficiente numérico Parte literal4a³b²2xyz7aabx² 3/4 x
Reducción de términos semejantes
1. Reduce los términos semejantes:a) 5a + 7a + 4ab) 4x + 5x 2x + xc) 12a 8a + 4a + ad) 9x 8y + 5y 2xe) 14x x 17y + 4x y + 23x 16yf) 7x + 4x² + 5x + 9x²2. Resuelve los paréntesis y luego reduce los términos semejantes:a) (9a 4b) + (3a 2b)b) (3a + b) (2a b)c) (x 3y + 5z) (4x + 3y 8z)
d) [9a (3a + 7) + (6 + 4a)] (a + b)e) [8 + (2x 1)] + [(6x 5) 2]
Ecuaciones sencillas
1. Resolver las siguientes ecuaciones de primer grado:1. 9 − z = 12. x +7 = 153. 7 − x = −14. x + 9 = 165. z − 15 = 36 z
2.
Resuelve las siguientes ecuacionesa) 3x – 2 = x + 6b) 5 (x+3) – 4 (3x – 3) = 203. Resuelve la ecuaciones:a)b)c)d)4. Resuelve la ecuación:5. Resuelve la ecuación:
Más ecuaciones
. Halla la solución de las ecuaciones siguientes:a)
( ) ( )
12354326
-- = -+
x x
A) Traduce a lenguaje algebraico:
1. El triple de un número.
2. La mitad del resultado de sumarles al triple de un número 4 unidades.
3. La diferencia de los cuadrados de dos números de dos números consecutivos.
4. Cinco veces el resultado de restarle al doble de un número 5 unidades
Solución: 5(2x-5)
5. Expresa algebraicamente el área y el perímetro de un cuadrado de lado x.
x
 B) Asocia cada una de los enunciados con la expresión algebraica que le corresponde: B) Asocia cada una de los enunciados con la expresión algebraica que le corresponde:
|
1) La suma de los cuadrados de dos números
|
|
|
2) El espacio recorrido por un móvil es igual a su velocidad por el tiempo que está en movimiento
|
|
|
3) El área del circulo de radio x
|
(x +y)2= x2+ y2+ 2xy
|
|
4) Los lados de un triángulo son proporcionales a 2, 3 y 5
|
E = v .t
|
|
5) El cuadrado de la suma de dos números es igual a la suma de sus cuadrados más el doble de su producto
|
x2+ y2 (1)
|
|
6) Media aritmética de tres números
|
Px2
|
C) Calcula el valor numérico de las siguientes expresiones para los valores que se indican:
1. 2x +1 para x =0
2. x2 + y2 para x =1 , y =3
3. (1-2x)(1+ 2x) para x = 2
4. 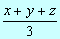 para x =3, y =2, z =4 para x =3, y =2, z =4
Solución 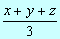 = =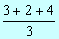 =3 =3
5. x2+ y2+ 2xy para x =1, y =2
6. –2x2y3 para x =2, y = 2
D) Identidades notables.
Cuadrado de una suma 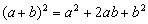
Cuadrado de una diferencia 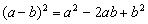
Diferencia de cuadrados 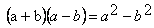
1) Desarrolla las siguientes expresiones:
a) (x +2)2
b) (x -1)2
c) (2x +3)2
d) (x +2)(x –2)
e) (2x –1)(2x +1)
f) (3x – y)2
g) (2x –3y)(2x +3y) = 4x2 –9y2
h) (x -1)3
i) (x +5)2-(x-3)2
2) Factoriza las siguientes expresiones algebraicas:
a) 3x4 -2x2
b) x2 –1
c) x2 +6x +9
Solución. No tiene ningún factor común , es una identidad notable: (x +3)2= x2 +6x +9
d) x2 + 4 +4x
e) 4x2-y2
f) 9 –6x +x2
g) 2x –4x2y
h) x2 +x y +x z +y z
Solución: x(x +y) +z(x +y) =(x +z) (x + y)
i) a x –ay –b x +by
3) Completa las siguientes expresiones para que sean cuadrados perfectos
a) x2+ 2x+.....
b) 4x2 + 8x+......
Solución: 4x2 + 8x +4 = (2x +2)2
c) 9x2 -....+ 16
E) Calcula el grado de los siguientes polinomios:
1. –2x2y3 2. . x2+ y2+ 2xy
3. 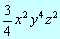 Solución: 2+4+2 =8 Solución: 2+4+2 =8
4. (x +5)2-(x-3)2
5. 7x5-3x2-6x4+2+x
F) Efectúa las operaciones indicadas y simplifica la expresión resultante.
1) 3(x3 –5x +7) –(2x3 +6x2 +11x+4)
2) 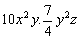
3) 2x(4x2 –6x +2) +3 (5x2 –3x-4)- 14 x2
4) (3x3 –x + 5) (2x3 +1)
5) (x3y3 + 2) (x3y3 - 2)
6) (7x3 –5x+3) (2x2 +x-1)
7) 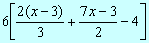
Solución: 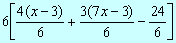 = 4x-12 +21x-9-24 = 25x -45 = 4x-12 +21x-9-24 = 25x -45
8) 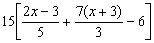
9) 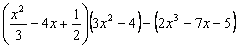
G) Operaciones con expresiones algebraicas:
1) Multiplica la siguiente expresión por 12 y simplifica el resultado:
2) Multiplica por 20 y simplifica el resultado:
H) Divide los siguientes polinomios:
1) 15 a3b2c : 6 a2c =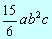 = =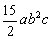
2) 5 x3y2z4 : 3 x2z2
3) (2x3 +6x2 +11x+4):(x +1)
4) (2x3 +6x2 +11x+4) : (x-3)
5) (x4 -6x3 +5x2-4x+1): (x2 –x +5)
6) (x3 +6x2 +5x+4): (x2 –3x +1)
 Solución Solución
x3 + 6x2 +5x +4 x2 –3x +1
-x3 +3x2 -x x +9
/ 9x2 + 4x +4
-9x2 + 27x-9
/ 31x –5
7) (x4 -5x3 +3x2-2x+5): (x2 +x -3)
Nota. Cuando el divisor es un binomio de la forma (x-a) se puede aplicar la regla de Ruffini, que utiliza sólo los coeficientes
Ejemplo. Divide x3-3x2+ 5x-7 entre (x-3)
Se hace la siguiente disposición de la figura.
El cociente es x2+5 y el resto 8
1) (x3 –x2 -16x -3): (x -3)
Solución: Utilizando Ruffini quedaría
Nos queda que el cociente es x2 +2x – 10 y el resto -33
2) (2x3 +6x2 +11x+4):(x +1)
3) (3x4 +6x2 +11x+4) : (x-2)
4) (x3 + 1) : (x +1)
5) (–x4 +2x3 +5x -3):(x+3)
Ampliación
Teorema del resto.
El resto de la división de un polinomio P(x) entre el binomio (x-a) es el valor numérico del polinomio en x =a, es decir el resto es el valor de P al sustituir la x por a,
R =P(a).
Ejemplo: El resto de la división ( x3 -2x2 +3x -4):(x-1) es:
13-2.12+3.1-4=1-2+3-4= -2 (comprobarlo)
1. Calcula el resto de la división (x3 –x2 -16x -3): (x -3) sin efectuarla
2.Calcula el valor de k para que la división de P(x) entre Q(x) dé exacta:
a) P(x) = x3 -x2 +k.x -4, Q(x) = (x-2)
b) P(x) = x4 -2x3 +3x2 –k x -5; Q(x) = (x +1)
2. Calcula el valor de k, para que el resto de la división del polinomio x4 –k x3 +3x2 – x +4 entre el binomio x +2 nos dé15.
Factorización
Factorizar un polinomio es ponerle como producto de sus factores (se llama también descomposición en factores del polinomio).
Para factorizar hay que tener en cuenta las identidades notables, el sacar factor común, la regla de Ruffini, y la resolución de ecuaciones (de 2º grado) para la búsqueda de raíces.
Ejemplo: Factoriza x3-5x2+ 4x
Solución
En primer lugar se saca factor común x, x3-5x2+ 4x =x(x2-5x+4)
El segundo factor es un polinomio de 2º grado, y para encontrar los otros factores se puede obtener las raíces aplicando la fórmula de la ecuación de 2º grado.
x = 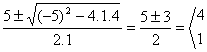 por tanto los factores son (x-4) y (x-1) El polinomio factorizado es: x(x-4)(x-1).
Nota: También podría haberse usado Ruffini para el cálculo de las raíces, ya que son enteras
d) x3 -11x2 +34x -24
e) x4 -11x3 +33x2 -9x -54
Si necesitas mas ejercicios del tema de polinomios visita estos enlaces
 Fracciones Algebraicas Fracciones AlgebraicasA) Hallar el valor numérico de las siguientes fracciones algebraicas en los puntos que se indican:
1) 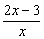 en x = 1, x =3. en x = 1, x =3.
2) 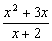 en x = 2, x = 0. en x = 2, x = 0.
4)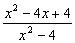 en x =-2, 0, 1 y 2 en x =-2, 0, 1 y 2
B) Estudia si las siguientes fracciones son equivalentes:
1) 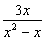 y y 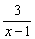
2) 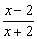 y y 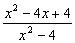
Solución. Se tiene:
(x-2)(x2-4) = x3 -4x -2x2+8 = x3 -2x2 -4x +8
(x +2)(x2-4x+4) = x3 -4x2 +4x+ 2x2 -8x +8 = x3 -2x2 -4x +8
Son equivalentes.
C) Simplifica las siguientes fracciones algebraicas, en los casos posibles:
1) 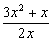
2) 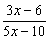
3) 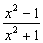
4)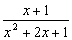
6) 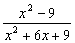
D) Realiza las operaciones indicadas y simplifica el resultado en los casos que se pueda.
1) 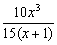 . .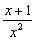
2) 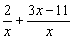
3)  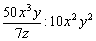
4) 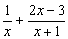
Solución. Primero reducimos a común denominador y después sumamos los numeradores:
m .c. m (x, x +1) = x(x +1) =x2+ x
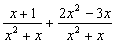 = =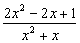
5) 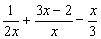
6) 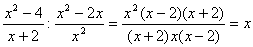
7) 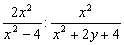
8)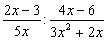
Si necesitas mas ejercicios del tema de polinomios visita estos enlaces |